Hyperbola is a curve

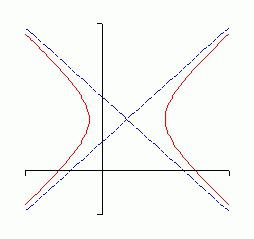
Geometric formation, which is calledhyperbola, is a plane curve of a second-order figure, consisting of two curves that are drawn separately and do not intersect. The mathematical formula for its description looks like this: y = k / x, if the number under the index k is not zero. In other words, the vertices of the curve tend to zero, but they will never intersect with it. From the point of view of the point construction, the hyperbola is the sum of the points on the plane. Each such point is characterized by a constant magnitude of the modulus of the difference in distance from the two focal centers.

A flat curve is distinguished by the main features that are inherent only to it:

• Hyperbola are two separate lines, called branches.
• In the middle of an axis of great order is the center of the figure.
• The vertex is the point of two branches nearest each other.
• The focal distance denotes the distance from the center of the curve to one of the foci (denoted by the letter "c").
• The major axis of the hyperbola describes the shortest distance between the branch lines.
• The foci lie on the major axis, provided that the distance from the center of the curve is the same. The line that supports the major axis is called the transverse axis.
• The semimajor axis is the calculated distance from the center of the curve to one of the vertices (denoted by the letter "a").
• A straight line that runs perpendicular to the transverse axis through its center is called the conjugate axis.
• The focal parameter defines the segment between the focus and the hyperbola perpendicular to its transverse axis.
• The distance between the focus and the asymptote is called the impact parameter and is usually encoded in the formulas under the letter "b".

In classical Cartesian coordinates, the well-known equation by which a hyperbola can be constructed looks like this: (x²/a²) - (y²/at²) = 1. The type of curve that has the same semi-axis is called equilateral. In a rectangular coordinate system, it can be described by a simple equation: xy = a²/ 2, and the focus of the hyperbola should be located at the intersection points (a, a) and (-a, -a).

Each curve can have a parallelhyperbola. This is its conjugate variant, in which the axes change places, and the asymptotes remain in place. The optical property of the figure is that light from an imaginary source in one focus is able to reflect the second branch and intersect in the second focus. Any point of a potential hyperbola has a constant value of the ratio of the distance to any focus to the distance to the director. A typical flat curve can exhibit both a mirror and rotational symmetry when rotated 180 ° in the center.

The eccentricity of the hyperbola is determined by the numericalthe characteristic of the conic section, which shows the degree of deviation of the section from the ideal circle. In mathematical formulas, this indicator is denoted by the letter "e". Eccentricity is usually invariant with respect to the motion of the plane and the process of transforming its similarity. Hyperbola is a figure in which the eccentricity is always equal to the ratio between the focal length and the major axis.