Одной из важнейших наук, применение которой можно to see in such disciplines as chemistry, physics, and even biology, is mathematics. The study of this science allows you to develop some mental qualities, improve abstract thinking and the ability to concentrate. One of the topics that deserve special attention in the “Mathematics” course is the addition and subtraction of fractions. For many students, learning it is difficult. Perhaps our article will help to better understand this topic.
How to subtract fractions whose denominators are the same
Fractions are the same numbers with which you canperform various actions. They differ from integers in the presence of a denominator. That is why when performing actions with fractions you need to learn some of their features and rules. The simplest case is subtraction of ordinary fractions, the denominators of which are represented in the form of the same number. Perform this action is not difficult if you know a simple rule:
- To subtract one from one fraction,It is necessary to subtract from the numerator of the reduced fraction the numerator of the subtracted fraction. This number is written to the numerator of the difference, and the denominator is left the same: k / m - b / m = (k-b) / m.

Examples of subtraction fractions, the denominators of which are the same
Consider how this looks in an example:
7/19 - 3/19 = (7 - 3) / 19 = 4/19.
From the numerator of the reduced fraction "7" subtractthe numerator of the subtracted fraction "3", we get "4". We write this number in the numerator of the answer, and in the denominator we put the same number as in the denominators of the first and second fractions - "19".
The picture below shows some more similar examples.

Consider a more complex example where fractions with the same denominators are subtracted:
29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29 - 3 - 8 - 2 - 7) / 47 = I / 47.
From the numerator of the reduced fraction "29" subtracting bythe queue numerators of all subsequent fractions are “3”, “8”, “2”, “7”. As a result, we get the result "9", which we write down in the numerator of the answer, and in the denominator we write down the number that is in the denominators of all these fractions, - "47".
Addition of fractions with the same denominator
The addition and subtraction of ordinary fractions is carried out on the same principle.
- In order to add fractions whose denominators are the same, it is necessary to add the numerators. The resulting number is the numerator of the sum, and the denominator remains the same: k / m + b / m = (k + b) / m.
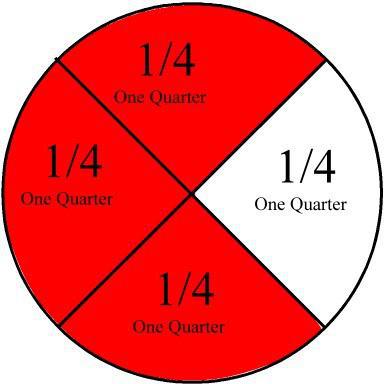
Consider how this looks in an example:
1/4 + 2/4 = 3/4.
To the numerator of the first term of the fraction - "1" -add the numerator of the second term of the fraction - "2". The result is “3” - we write the sum in the numerator, and the denominator is the same as in fractions, “4”.

Fractions with different denominators and their subtraction
Action with fractions that have the samedenominator, we have already reviewed. As we see, knowing simple rules, it is quite easy to solve such examples. But what if you need to perform an action with fractions that have different denominators? Many high school students are confronted by such examples. But even here, if you know the principle of the solution, the examples will no longer be difficult for you. There is also a rule here, without which the solution of such fractions is simply impossible.
To subtract fractions with different denominators, you need to bring them to the same lowest denominator.

We'll talk more about how to do this.
Fraction property
In order for a few fractions to result inthe same denominator, you need to use the main property of the fraction in the solution: after dividing or multiplying the numerator and denominator by the same number, you get a fraction equal to this one.
So, for example, a fraction 2/3 can have suchdenominators like "6", "9", "12", etc., that is, it can be of the form of any number that is a multiple of "3". After the numerator and denominator we multiply by “2”, we get a fraction 4/6. After the numerator and denominator of the original fraction are multiplied by "3", we get 6/9, and if we perform the same action with the number "4", we get 8/12. In one equality, this can be written as:
2/3 = 4/6 = 6 / i = 8/12 ...
How to bring several fractions to the same denominator
Consider how to bring a few fractions tothe same denominator. For example, take the fractions shown in the picture below. First you need to determine what number can be the denominator for all of them. To facilitate the decomposition of the existing denominators into factors.
Знаменатель дроби 1/2 и дроби 2/3 на множители can not be decomposed. The denominator 7/9 has two factors 7/9 = 7 / (3 x 3), the denominator of the fraction 5/6 = 5 / (2 x 3). Now it is necessary to determine which factors will be the smallest for all these four fractions. Since the first fraction in the denominator has the number “2”, it means that it must be present in all denominators, there are two triples in the 7/9 fraction, which means that they must both be present in the denominator. Given the above, we determine that the denominator consists of three factors: 3, 2, 3 and is equal to 3 x 2 x 3 = 18.

Consider the first fraction - 1/2.In its denominator there is a “2”, but there is not a single number “3”, and there should be two. To do this, we multiply the denominator by two triples, but, according to the property of a fraction, we and the numerator must multiply by two triples:
1/2 = (1 x 3 x 3) / (2 x 3 x 3) = 9/18.
Similarly, we perform actions with the remaining fractions.
- 2/3 - the denominator lacks one three and one two:
2/3 = (2 x 3 x 2) / (3 x 3 x 2) = 12/18. - 7/9 or 7 / (3 x 3) - the denominator does not have two:
7/9 = (7 x 2) / (9 x 2) = 14/18. - 5/6 or 5 / (2 x 3) - in the denominator there is not a triple:
5/6 = (5 x 3) / (6 x 3) = 15/18.
All together it looks like this:

How to subtract and add fractions with different denominators
As mentioned above, in order tomake addition or subtraction of fractions with different denominators, they must be brought to the same denominator, and then use the rules for subtracting fractions that have the same denominator, which has already been described.
Consider this with an example: 4/18 - 3/15.
Find a multiple of the numbers 18 and 15:
- The number 18 consists of 3 x 2 x 3.
- The number 15 consists of 5 x 3.
- The total multiple will consist of the following factors 5 x 3 x 3 x 2 = 90.
After the denominator is found,it is necessary to calculate the multiplier, which will be excellent for each fraction, that is, the number by which not only the denominator, but also the numerator must be multiplied. For this, the number we have found (the common multiple) is divided by the denominator of the fraction in which you need to determine additional factors.
- 90 divided by 15. The resulting number "6" will be a multiplier for 3/15.
- 90 divided by 18. The resulting number "5" will be a multiplier for 4/18.
The next stage of our decision is the reduction of each fraction to the denominator "90".
How this is done, we have already said. Consider how this is written in the example:
(4 x 5) / (18 x 5) - (3 x 6) / (15 x 6) = 20/90 - 18/90 = 2/90 = 1/45.
If fractions with small numbers, then you can determine the common denominator, as in the example shown in the picture below.

Similarly, the addition of fractions with different denominators is made.
Subtraction and addition of fractions with whole parts
Subtraction fractions and their addition, we have already disassembled in detail. But how to produce a subtraction if a fraction has an entire part? Again, use several rules:
- All fractions with integer part translate towrong. In simple words, remove the whole part. To do this, multiply the number of the integer part by the denominator of the fraction, add the resulting product to the numerator. The number that will be obtained after these actions is the numerator of an irregular fraction. The denominator remains the same.
- If fractions have different denominators, you should bring them to the same.
- Add or subtract with the same denominators.
- When receiving an improper fraction, select the whole part.

There is another way by which you cancarry out the addition and subtraction of fractions with whole parts. For this, separate actions with whole parts are performed, and separate actions with fractions, and the results are recorded together.

The given example consists of fractions whichhave the same denominator. In the case when the denominators are different, they must be brought to the same, and then follow the steps as shown in the example.
Subtract fractions from integer
Еще одной из разновидностей действий с дробями is the case when the fraction must be subtracted from the natural number. At first glance, such an example seems difficult to solve. However, everything is pretty simple here. To solve it, it is necessary to convert an integer to a fraction, and with such a denominator, which is in the subtracted fraction. Next, produce a subtraction, similar to the subtraction with the same denominators. For example, it looks like this:
7 - 4/9 = (7 x 9) / 9 - 4/9 = 53/9 - 4/9 = 49/9.
Приведенное в этой статье вычитание дробей (6 class) is the basis for solving more complex examples that are considered in subsequent classes. Knowledge of this topic is subsequently used to solve functions, derivatives, and so on. Therefore, it is very important to understand and understand the actions with fractions discussed above.