Differential calculi of a function of one and several variables

Differential calculus is a section of mathematical analysis that studies the derivative, differentials and their use in the study of a function.

History of appearance

Differential Calculus stood out inan independent discipline in the second half of the 17th century, thanks to the works of Newton and Leibniz, who formulated the main provisions in calculating the differentials and noticed the links between integration and differentiation. Since then, the discipline has developed along with the calculation of integrals, thereby forming the basis of mathematical analysis. The emergence of data calculi opened a new modern period in the mathematical world and caused the emergence of new disciplines in science. Also expanded the possibility of applying mathematical science in science and technology.

Basic concepts

Differential Calculus is based onfundamental concepts of mathematics. They are: real number, continuity, function and limit. After a while they took the modern look, thanks to integral and differential calculi.

Process of creation

Formation of differential calculus in the formapplied, and then the scientific method occurred before the emergence of philosophical theory, which was created by Nikolai Kuzansky. His works are considered an evolutionary development from the judgments of ancient science. Despite the fact that the philosopher himself was not a mathematician, his contribution to the development of mathematical science is undeniable. Cusa was one of the first to leave arithmetic as the most accurate field of science, putting the mathematics of that time under doubt.

In ancient mathematicians universal criterionthere was a unit, while the philosopher offered as a new measure infinity to replace the exact number. In this connection, the representation of accuracy in mathematical science is inverted. Scientific knowledge, in his view, is divided into rational and intellectual. The second is more accurate, according to the scientist, since the first gives only an approximate result.

Idea

The basic idea and concept in differentialCalculus associated with the function in small neighborhoods of certain points. To do this, it is necessary to create a mathematical apparatus for studying a function whose behavior in a small neighborhood of established points is close to the behavior of a polynomial or a linear function. It is based on the definition of the derivative and the differential.

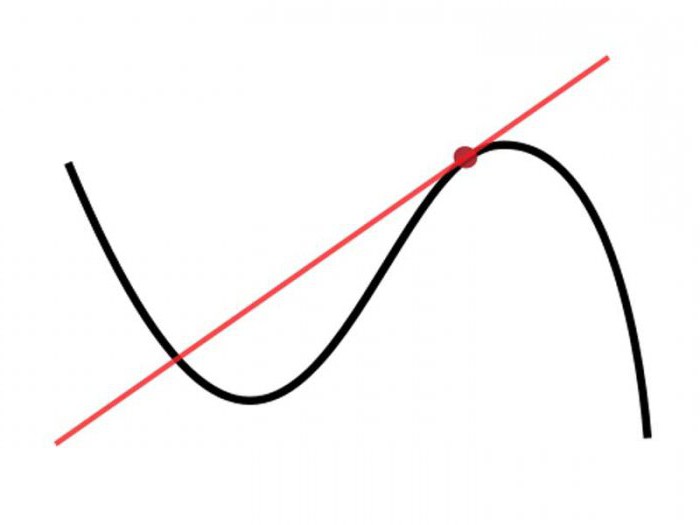
The emergence of the concept of a derivative was caused by a large number of problems from the natural sciences and mathematics, which led to finding the values ​​of the limits of one type.

One of the main tasks that are given asAn example, starting from high school, is to determine the speed of a point in a straight line and build a tangent line to this curve. The differential is connected with this, since it is possible to approximate a function in a small neighborhood of the point of the linear function under consideration.

Compared to the concept of the derivative functionreal variable, the definition of differentials simply goes to a function of a general nature, in particular to the image of one Euclidean space to another.

Derivative

Пусть точка движется по направлению оси Оу, за take time x, which is measured from a certain beginning of the moment. Such a movement can be described by the function y = f (x), which is assigned to each time moment x coordinate of the moving point. In mechanics, this function should be called the law of motion. The main characteristic of motion, especially non-uniform, is instantaneous speed. When a point moves along the axis Oy according to the law of mechanics, then at a random time moment x it acquires the coordinate f (x). At the time moment x + Δх, where Δх denotes the time increment, its coordinate will be f (x + Δx). Thus, the formula Δy = f (x + Δx) - f (x) is formed, which is called the function increment. It represents the path traveled by the point in the time from x to x + Δx.

Due to the occurrence of this speed at the momenttime derivative is introduced. In an arbitrary function, the derivative at a fixed point is called the limit (if it exists). It can be indicated by certain characters:

f ’(x), y’, ý, df / dx, dy / dx, Df (x).

The process of calculating the derivative is called differentiation.

Differential calculus of functions of several variables

This method of calculus will be applied whenresearch function with multiple variables. In the presence of two variables x and y, the partial derivative with respect to x at point A is called the derivative of this function with respect to x with fixed y.

May be indicated by the following symbols:

f ’(x) (x, y), u’ (x), ∂u / ∂x or ∂f (x, y) ’/ ∂x.

Required skills

Чтобы успешно изучить и уметь решать диффуры, skills in integration and differentiation are required. To make it easier to understand the differential equations, one should well understand the topic of the derivative and the indefinite integral. It also does not hurt to learn how to search for a derivative of an implicitly given function. This is due to the fact that in the process of studying it is often necessary to use integrals and differentiation.

Types of differential equations

Practically in all test papers related to differential equations of the first order, there are 3 types of equations: homogeneous, with separable variables, linear inhomogeneous.

There are more rare types of equations: with full differentials, Bernoulli equations, and others.

Solution Basics

First, remember algebraicequations from the school course. They contain variables and numbers. To solve an ordinary equation, one should find a set of numbers satisfying a given condition. As a rule, such equations had the same root, and to verify the correctness, one had only to substitute this value for the place of the unknown.

Differential equation is similar. In general, such a first order equation includes:

• Independent variable.
• Derivative of the first function.
• Function or dependent variable.

In some cases, one of theunknowns, x or y, but this is not so important, since the presence of the first derivative is necessary, without higher order derivatives, so that the solution and differential calculus are correct.

Solving a differential equation means finding the set of all functions that match a given expression. Such a set of functions is often called a general solution of the DU.

Integral calculus

Integral calculus is one of the sections of mathematical analysis, which studies the concept of an integral, properties and methods of its calculation.

Often the calculation of the integral occurs whencalculating the area of ​​the curved shape. By this area is meant the limit to which the area of ​​a polygon inscribed into a given figure tends with a gradual increase in its side, while these parties can be fulfilled less than any previously specified arbitrary small value.

The main idea in calculating the area of ​​arbitrarya geometric figure consists in calculating the area of ​​a rectangle, that is, proving that its area is equal to the product of length and width. When it comes to geometry, all constructions are made using a ruler and compass, and then the ratio of length to width is a rational value. When calculating the area of ​​a right-angled triangle, it can be determined that if we put the same triangle next to it, a rectangle is formed. In a parallelogram, the area is calculated by a similar, but slightly more complicated method, through a rectangle and a triangle. In polygons, an area is counted through the triangles it contains.

When determining the area of ​​an arbitrary curve givenThe method will not work. If you break it into single squares, then there will be empty spaces. In this case, they try to use two covers, with rectangles on the top and bottom, as a result, those include the graph of the function and do not include. The important thing here is the method of splitting into these rectangles. Also, if we take the breaking up more and more decreasing, then the area above and below should converge on a certain value.

Should return to the method of dividing into rectangles. There are two popular methods.

Riemann formalized the definition of an integral,created by Leibniz and Newton, as square subgraphs. In this case, the figures were considered, consisting of a number of vertical rectangles and obtained by dividing the segment. When reducing the break, there is a limit to which the area of ​​a similar figure is reduced, this limit is called the Riemann integral of the function on a given segment.

The second method is the construction of the integralLebesgue, consisting in the fact that for the place of division of the designated area into parts of the integrand and then compiling the integral sum of the values ​​obtained in these parts, its range of values ​​is divided into intervals, and then summed with the corresponding measures of the inverse images of these integrals.

Modern benefits

One of the basic study guidesof differential and integral calculus was written by Fichtengolts - "Course of differential and integral calculus". His textbook is a fundamental tool for the study of mathematical analysis, which has sustained many publications and translations into other languages. It was created for university students and has been used in many educational institutions for a long time as one of the main study aids. Gives theoretical data and practical skills. First published in 1948.

Function investigation algorithm

In order to investigate a function using the methods of differential calculus, it is necessary to follow an already specified algorithm:

1. Find the domain of the function.
2. Find the roots of a given equation.
3. Calculate the extremes. To do this, calculate the derivative and the point where it equals zero.
4. Substitute the obtained value into the equation.

Varieties of Differential Equations

Do first-order control (otherwise, the differential calculus of one variable) and their types:

• Equation with separable variables: f (y) dy = g (x) dx.
• The simplest equations, or the differential calculus of a single variable function, have the formula: y "= f (x).
• Linear inhomogeneous DE of the first order: y "+ P (x) y = Q (x).
• Bernoulli differential equation: y "+ P (x) y = Q (x) y^a .
• Equation with full differentials: P (x, y) dx + Q (x, y) dy = 0.

Second-order differential equations and their types:

• Linear homogeneous differential equation of the second order with constant values ​​of the coefficient: y^Mr.+ py "+ qy = 0 p, q belongs to R.
• Linear inhomogeneous differential equation of the second order with a constant value of the coefficients: y^Mr.+ py "+ qy = f (x).
• Linear homogeneous differential equation: y^Mr.+ p (x) y "+ q (x) y = 0, and a second order nonhomogeneous equation: y^Mr.+ p (x) y "+ q (x) y = f (x).

Differential equations of higher orders and their types:

• Differential equation that can be reduced in order: F (x, y^(to),and^{(to + 1)}.., y⁽ⁿ⁾= 0
• Higher order linear equation homogeneous: and⁽ⁿ⁾+ f_(n-1)and^(n-1)+ ... + f₁y "+ f₀y = 0and heterogeneous: and⁽ⁿ⁾+ f_(n-1)and^(n-1)+ ... + f₁y "+ f₀y = f (x).

Stages of solving a problem with a differential equation

With the help of remote control, not only mathematicalor physical issues, but also various problems from biology, economics, sociology and other things. Despite the great variety of topics, one should follow a single logical sequence when solving such problems:

1. Drafting of control.One of the most difficult stages, which requires maximum accuracy, since any mistake will lead to completely wrong results. All factors affecting the process should be considered and initial conditions should be determined. It should also be based on facts and logical conclusions.
2. The solution of the composed equation. This process is simpler than the first point, since it requires only rigorous execution of mathematical calculations.
3. Analysis and evaluation of the results. The derived solution should be evaluated to establish the practical and theoretical value of the result.

An example of the use of differential equations in medicine

The use of remote control in the field of medicine occurswhen building an epidemiological mathematical model. It should not be forgotten that these equations are also found in biology and chemistry, which are close to medicine, because research of various biological populations and chemical processes in the human body plays an important role in it.

In the given example of an epidemic, one can consider the spread of infection in an isolated society. Inhabitants are divided into three types:

• Infected, the number of x (t), consisting of individuals, carriers of infection, each of which is infectious (the incubation period is short).
• The second type includes susceptible individuals y (t) that can become infected when they come in contact with the infected.
• The third species includes immunities of z (t), which are immune or died due to illness.

The number of individuals is constant, accounting for birth, natural death and migration is not counted. At the core there will be two hypotheses.

The percentage of incidence in a certain temporarythe moment equals x (t) y (t) (based on the assumption that the number of cases is proportional to the number of intersections between patients and susceptible representatives, which in the first approximation will be proportional to x (t) y (t)) increases, and the number of susceptible decreases with speed, which is calculated by the formula ax (t) y (t) (a> 0).

The number of immune individuals that have acquired immunity or died increases at a rate that is proportional to the number of cases, bx (t) (b> 0).

As a result, you can create a system of equations with all three indicators and on the basis of its conclusions.

An example of use in economics

Differential calculus is often used wheneconomic analysis. The main task in economic analysis is the study of values ​​from the economy, which are recorded in the form of a function. This is used to solve problems like changing incomes immediately after increasing taxes, introducing duties, changing the company's revenue when the cost of products changes, in what proportion can be replaced with new equipment. To solve such questions, it is required to construct a link function from incoming variables, which are then studied using differential calculus.

In the economic sphere it is often necessary to findthe most optimal indicators: maximum labor productivity, highest income, lowest costs and so on. Each such indicator is a function of one or more arguments. For example, production can be viewed as a function of the costs of labor and capital. In this connection, finding the appropriate value can be reduced to finding the maximum or minimum of a function from one or several variables.

Such tasks create a class of extremeproblems in the economic field, which require differential calculus. When an economic indicator needs to be minimized or maximized as a function of another indicator, then at the maximum point the ratio of the function increment to the arguments tends to zero if the increment of the argument tends to zero. Otherwise, when such a relationship tends to some positive or negative value, the specified point is not suitable, because with increasing or decreasing the argument, you can change the dependent value in the desired direction. In the terminology of differential calculus, this will mean that the required condition for the maximum of a function is the zero value of its derivative.

In economics, there are often tasks onfinding the extremum of a function with several variables, because economic indicators are made up of many factors. Similar questions are well studied in the theory of functions of several variables using the methods of differential computation. Such tasks include not only maximized and minimized functions, but also limitations. Similar questions relate to mathematical programming, and they are solved using specially developed methods, also based on this branch of science.

Among the methods of differential calculus,used in economics, an important section is the marginal analysis. In the economic sphere, this term refers to a set of research methods for changing indicators and results when changing the volume of production, consumption, based on the analysis of their marginal indicators. The limiting index is considered to be the derivative or partial derivatives with several variables.

Differential calculus of several variables- An important topic in the field of mathematical analysis. For detailed study, you can use a variety of textbooks for higher education. One of the most famous created Fikhtengolts - "Course of differential and integral calculus." As is evident from the name, skills in working with integrals are of considerable importance for solving differential equations. When the differential calculus of a single variable function takes place, the solution becomes simpler. Although, it should be noted, it obeys the same basic rules. In practice, to investigate the function of differential calculus, it suffices to follow the already existing algorithm, which is given in high school and is only slightly complicated when entering new variables.